Információk és Szabályzat!

Pontos leírás:
Ezen a linken

A Lights Out egy elektronikus játék, amit a Tiger Electronics adott ki 1995-ben. A játék egy 5x5-ös fényekből álló rácsot tartalmaz. Amikor a játék elkezdődik, egy véletlenszerű vagy előre elmentett fényképet kapcsolnak be. Bármelyik fény megnyomásával be- és kikapcsolható, valamint a szomszédos fények is be- és kikapcsolódnak. A játék célja, hogy minél kevesebb gombnyomással lekapcsoljuk az összes fényt.

A Merlin, egy hasonló elektronikus játék, a Parker Brothers által került piacra az 1970-es években. Egy 3x3-as rácsot használt hasonló szabályokkal. Egy másik hasonló játékot a Vulcan Electronics gyártott 1983-ban XL-25 néven. A Tiger Toys is kiadott egy kártyás változatot a Lights Out játékról a Game com handheld játékkonzoljához 1997-ben, amelyet ingyen szállítottak a konzollal.

Azóta több új puzzle játék jelent meg a Lights Out-hoz hasonlóan, mint például a Lights Out 2000 (5x5-ös rács több színnel), a Lights Out Cube (hat 3x3-as lap hatással a szélekre), és a Lights Out Deluxe (6x6-os rács).

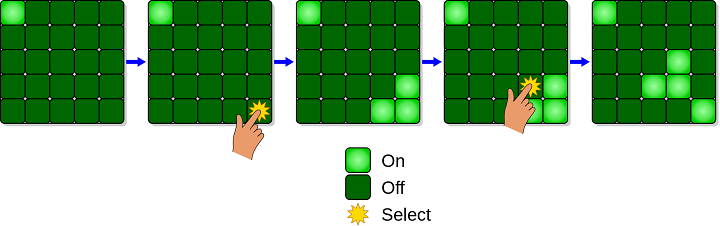
• Játékmenet

  A játék egy 5x5-ös fényekből álló rácsot tartalmaz.
  Amikor a játék elkezdődik, egy véletlenszerű vagy előre elmentett fényképet kapcsolnak be.
  Bármelyik fény megnyomásával be- és kikapcsolható, valamint a szomszédos fények is be- és kikapcsolódnak.
  A játék célja, hogy minél kevesebb gombnyomással lekapcsoljuk az összes fényt.

• Matematika

  Ha egy lámpa világít, akkor páratlan számú kapcsolással lehet kikapcsolni. Ha egy lámpa ki van kapcsolva, akkor páros számú kapcsolással lehet kikapcsolt állapotban tartani (ideértve a nulla kapcsolást is).
  A játék stratégiájában számos következtetést lehet levonni.
  Először is, nem számít, milyen sorrendben nyomják meg a lámpákat, mert az eredmény ugyanaz lesz.
  Másodszor, egy minimális megoldásban minden lámpát csak egyszer kell megnyomni, mert ha egy lámpát kétszer nyomnak meg, az ekvivalens az egyszeri megnyomással.
  1998-ban Marlow Anderson és Todd Feil lineáris algebrát használtak annak bizonyítására, hogy nem minden konfiguráció megoldható, és azt is bebizonyították, hogy bármely megoldható 5x5-ös feladványra pontosan négy győztes helyzet létezik, redundáns lépések nélkül.
  Az 5x5-ös Lights Out rácson egy 25x1 oszlopvektorral lehet reprezentálni, ahol a 1 és 0 a felkapcsolt és lekapcsolt állapotot jelöli. Minden elem az Z2 mező eleme, az egész számok Z osztályának modulusa 2.
  Anderson és Feil azt találták, hogy egy konfiguráció megoldható legyen (a nullvektort kiindulási konfigurációból származtatva), az alábbi N1 és N2 vektorokkal ortogonálisnak kell lennie (amelyeket 5x5-ös tömbként ábrázoltak, de nem szabad összetéveszteni mátrixokkal).
  
  

• Következtetés

  Ha egyszer találtunk egy megoldást, a minimális lépésszámmal járó megoldást kiválaszthatjuk azáltal, hogy kizárjuk a redundáns gombnyomáskészleteket, amelyeknek nincs kumulatív hatásuk.
  Ha az 5×5-ös puzzle nem oldható meg a játék szabályainak megfelelően, akkor a alsó sor bal oldali két fénye világos marad, amikor az összes többi fény kikapcsolt.
  A megoldások létezése bizonyított számos táblakonfigurációhoz, például hexagonálishoz, míg a n x n-es táblák megoldásai n≤200 esetében explicit módon fel vannak sorolva.
  Minden N × N esetre létezik megoldás. Az összefüggő gráfokon megoldható, ahol az egyik csúcsra való kattintás megfordítja annak értékét és szomszédjait. Általánosabban, ha az akció mátrix szimmetrikus, akkor annak diagonális eleme mindig megoldható.